2018大慶市中考數(shù)學(xué)模擬試題
一、選擇題:(每題3分,共30分)
1.下列運(yùn)算正確的是( )
A.a(chǎn)6÷a2=a3B.a(chǎn)6+a2=a8C.(a2)3=a6D.2a×3a=6a
2.已知地球上七大洲的總面積約為150000000km2,則數(shù)字150000000用科學(xué)記數(shù)法可以表示為( )
A.1.5×106B.1.5×107C.1.5×108D.1.5×109
3.在下列圖形中,既是軸對(duì)稱圖形,又是中心對(duì)稱圖形的是( )
A. B.
B. C.
C. D.
D.
4.若將函數(shù)y=2x2的圖象向右平行移動(dòng)1個(gè)單位,再向上平移5個(gè)單位,可得到的拋物線是( )
A.y=2(x﹣1)2﹣5B.y=2(x﹣1)2+5C.y=2(x+1)2﹣5D.y=2(x+1)2+5
5.雙曲線y=![]() (k≠0)經(jīng)過(1,﹣4),下列各點(diǎn)在此雙曲線上的是( )
(k≠0)經(jīng)過(1,﹣4),下列各點(diǎn)在此雙曲線上的是( )
A.(﹣1,﹣4)B.(4,1)C.(﹣2,﹣2)D.(![]() ,﹣4
,﹣4![]() )
)
6.如圖,點(diǎn)A、B、C是⊙O上的點(diǎn),若∠ACB=35°,則∠AOB的度數(shù)為( )
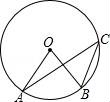
A.35°B.70°C.105°D.150°
7.如圖,為了測(cè)量河兩岸A、B兩點(diǎn)的距離,在與AB垂直的方向點(diǎn)C處測(cè)得AC=a,∠ACB=α,那么AB等于( )
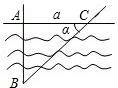
A.a(chǎn)?sinαB.a(chǎn)?tanαC.a(chǎn)?cosαD.![]()
8.如圖,△ABC中,∠ACB=70°,將△ABC繞點(diǎn)B按逆時(shí)針方向旋轉(zhuǎn)得到△BDE(點(diǎn)D與點(diǎn)A是對(duì)應(yīng)點(diǎn),點(diǎn)E與點(diǎn)C是對(duì)應(yīng)點(diǎn)),且邊DE恰好經(jīng)過點(diǎn)C,則∠ABD的度數(shù)為( )
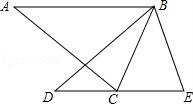
A.30°B.40°C.45°D.50°
9.如圖,直線l和雙曲線![]() (k>0)交于A、B兩點(diǎn),P是線段AB上的點(diǎn)(不與A、B重合),過點(diǎn)A、B、P分別向x軸作垂線,垂足分別是C、D、E,連接OA、OB、OP,設(shè)△AOC面積是S1,△BOD面積是S2,△POE面積是S3,則( )
(k>0)交于A、B兩點(diǎn),P是線段AB上的點(diǎn)(不與A、B重合),過點(diǎn)A、B、P分別向x軸作垂線,垂足分別是C、D、E,連接OA、OB、OP,設(shè)△AOC面積是S1,△BOD面積是S2,△POE面積是S3,則( )
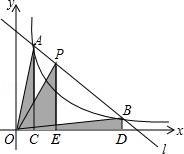
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
10.某油箱容量為60L的汽車,加滿汽油后行駛了100km時(shí),油箱中的汽油大約消耗了![]() ,如果加滿汽油后汽車行駛的路程為xkm,油箱中剩油量為yL,則y與x之間的函數(shù)解析式和自變量取值范圍分別是( )
,如果加滿汽油后汽車行駛的路程為xkm,油箱中剩油量為yL,則y與x之間的函數(shù)解析式和自變量取值范圍分別是( )
A.y=0.12x,x>0B.y=60﹣0.12x,x>0
C.y=0.12x,0≤x≤500D.y=60﹣0.12x,0≤x≤500
二、填空題:(每題3分,共30分)
11.在Rt△ABC中,∠C=90°,AC=4,AB=5,則sinB的值是 .
12.計(jì)算:![]() +
+![]() ﹣3
﹣3![]() = .
= .
13.把多項(xiàng)式2x2y﹣8xy2+8y3分解因式的結(jié)果是 .
14.不等式組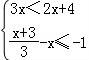 的解集是 .
的解集是 .
15.已知二次函數(shù)y=﹣x2+mx+2的對(duì)稱軸為直線x=![]() ,則m= .
,則m= .
16.已知扇形的圓心角為45°,弧長(zhǎng)為3π,則此扇形的半徑為 .
17.如圖,△ABC內(nèi)接于⊙O,∠BAC=120°,AB=AC,BD為⊙O的直徑,AD=6,則BC= .

18.點(diǎn)A是反比例函數(shù)y=![]() 第二象限內(nèi)圖象上一點(diǎn),它到原點(diǎn)的距離為10,到x軸的距離為8,則k= .
第二象限內(nèi)圖象上一點(diǎn),它到原點(diǎn)的距離為10,到x軸的距離為8,則k= .
19.已知:正方形ABCD的邊長(zhǎng)為2,點(diǎn)P是直線CD上一點(diǎn),若DP=1,則tan∠BPC的值是 .
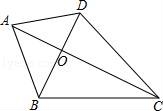
20.如圖,四邊形ABCD中,對(duì)角線AC⊥BD于點(diǎn)O,且AO=BO=4,CO=8,∠ADB=2∠ACB,則四邊形ABCD的面積為 .
三、解答題:(21、22題7分,23題、24題8分,25-27題各10分)
21.先化簡(jiǎn),再求代數(shù)式的值:![]() ,其中a=tan60°﹣2sin30°.
,其中a=tan60°﹣2sin30°.
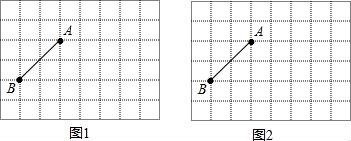
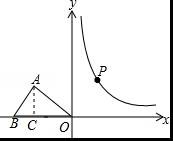
22.如圖,在小正方形的邊長(zhǎng)均為1的方格紙中,有線段AB,點(diǎn)A、B均在小正方形的頂點(diǎn)上.
(1)在圖1中畫一個(gè)以線段AB為一邊的平行四邊形ABCD,點(diǎn)C、D均在小正方形的頂點(diǎn)上,且平行四邊形ABCD的面積為10;
(2)在圖2中畫一個(gè)鈍角三角形ABE,點(diǎn)E在小正方形的頂點(diǎn)上,且三角形ABE的面積為4,tan∠AEB=![]() .請(qǐng)直接寫出BE的長(zhǎng).
.請(qǐng)直接寫出BE的長(zhǎng).
23.如圖,已知△ABC是等邊三角形,D、E分別在邊BC、AC上,且CD=CE,連接DE并延長(zhǎng)至點(diǎn)F,使EF=AE,連接AF、BE和CF.
(1)判斷四邊形ABDF是怎樣的四邊形,并說明理由;
(2)若AB=6,BD=2DC,求四邊形ABEF的面積.

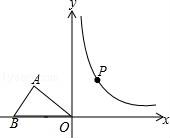
24.如圖,在平面直角坐標(biāo)系中,點(diǎn)O為坐標(biāo)原點(diǎn),△OAB的頂點(diǎn)B在x軸負(fù)半軸上,OA=OB=5,tan∠AOB=![]() ,點(diǎn)P與點(diǎn)A關(guān)于y軸對(duì)稱,點(diǎn)P在反比例函數(shù)y=
,點(diǎn)P與點(diǎn)A關(guān)于y軸對(duì)稱,點(diǎn)P在反比例函數(shù)y=![]() 的圖象上.
的圖象上.
(1)求反比例函數(shù)的解析式;
(2)點(diǎn)D在反比例函數(shù)y=![]() 第一象限的圖象上,且△APD的面積為4,求點(diǎn)D的坐標(biāo).
第一象限的圖象上,且△APD的面積為4,求點(diǎn)D的坐標(biāo).
25.工藝商場(chǎng)按標(biāo)價(jià)銷售某種工藝品時(shí),每件可獲利45元;按標(biāo)價(jià)的八五折銷售該工藝品8件與將標(biāo)價(jià)降低35元銷售該工藝品12件所獲利潤(rùn)相等.
(1)該工藝品每件的進(jìn)價(jià)、標(biāo)價(jià)分別是多少元?
(2)若每件工藝品按(1)中求得的進(jìn)價(jià)進(jìn)貨,標(biāo)價(jià)售出,工藝商場(chǎng)每天可售出該工藝品100件.若每件工藝品降價(jià)1元,則每天可多售出該工藝品4件.問每件工藝品降價(jià)多少元出售,每天獲得的利潤(rùn)最大?獲得的最大利潤(rùn)是多少元?
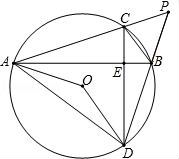
26.如圖,⊙O中弦AB⊥弦CD于E,延長(zhǎng)AC、DB交于點(diǎn)P,連接AO、DO、AD、BC.
(1)求證:∠AOD=90°+∠P;
(2)若AB平分∠CAO,求證:AD=AB;
(3)在(2)的條件下,若⊙O的半徑為5,PB=![]() ,求弦BC的長(zhǎng).
,求弦BC的長(zhǎng).
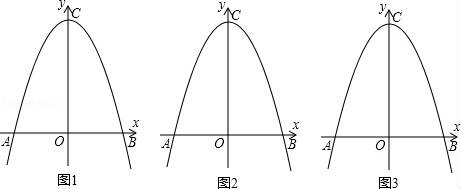
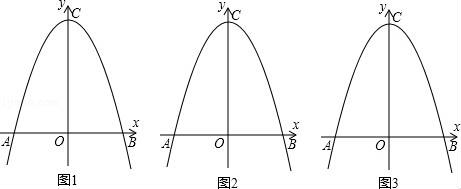
27.如圖所示,平面直角坐標(biāo)系中,O為原點(diǎn),拋物線y=﹣x2+2k(k≠0)頂點(diǎn)為C點(diǎn),拋物線交x軸于A、B兩點(diǎn),且AB=CO;
(1)求此拋物線解析式;
(2)點(diǎn)P為第一象限內(nèi)拋物線上一點(diǎn),連接PA交y軸于點(diǎn)D,連接PC,設(shè)點(diǎn)P的橫坐標(biāo)為t,△PCD的面積為S,求S與t的函數(shù)關(guān)系式,并直接寫出t的取值范圍;
(3)在(2)的條件下,連接AC,過點(diǎn)D作DE⊥y軸交AC于E,連接PE,交y軸于F,若5CF=3OF,求P點(diǎn)坐標(biāo).
2018大慶市中考數(shù)學(xué)模擬試題參考答案
一、選擇題:(每題3分,共30分)
1.下列運(yùn)算正確的是( )
A.a(chǎn)6÷a2=a3B.a(chǎn)6+a2=a8C.(a2)3=a6D.2a×3a=6a
【考點(diǎn)】單項(xiàng)式乘單項(xiàng)式;合并同類項(xiàng);冪的乘方與積的乘方;同底數(shù)冪的除法.
【分析】原式利用單項(xiàng)式乘以單項(xiàng)式法則,合并同類項(xiàng)法則,冪的乘方運(yùn)算法則,以及同底數(shù)冪的乘法法則計(jì)算得到結(jié)果,即可作出判斷.
【解答】解:A、原式=a4,錯(cuò)誤;
B、原式不能合并,錯(cuò)誤;
C、原式=a6,正確;
D、原式=6a2,錯(cuò)誤,
故選C
2.已知地球上七大洲的總面積約為150000000km2,則數(shù)字150000000用科學(xué)記數(shù)法可以表示為( )
A.1.5×106B.1.5×107C.1.5×108D.1.5×109
【考點(diǎn)】科學(xué)記數(shù)法—表示較大的數(shù).
【分析】科學(xué)記數(shù)法的表示形式為a×10n的形式,其中1≤|a|<10,n為整數(shù).確定n的值時(shí),要看把原數(shù)變成a時(shí),小數(shù)點(diǎn)移動(dòng)了多少位,n的絕對(duì)值與小數(shù)點(diǎn)移動(dòng)的位數(shù)相同.當(dāng)原數(shù)絕對(duì)值>1時(shí),n是正數(shù);當(dāng)原數(shù)的絕對(duì)值<1時(shí),n是負(fù)數(shù).
【解答】解:將150000000用科學(xué)記數(shù)法表示為1.5×108.
故選:C.
3.在下列圖形中,既是軸對(duì)稱圖形,又是中心對(duì)稱圖形的是( )
A. B.
B. C.
C. D.
D.
【考點(diǎn)】中心對(duì)稱圖形;軸對(duì)稱圖形.
【分析】根據(jù)軸對(duì)稱圖形與中心對(duì)稱圖形的概念分別分析求解.
【解答】解:A、不是軸對(duì)稱圖形,是中心對(duì)稱圖形,故此選項(xiàng)錯(cuò)誤;
B、是軸對(duì)稱圖形,不是中心對(duì)稱圖形,故此選項(xiàng)錯(cuò)誤;
C、是軸對(duì)稱圖形,也是中心對(duì)稱圖形,故此選項(xiàng)正確;
D、不是軸對(duì)稱圖形,也不是中心對(duì)稱圖形,故此選項(xiàng)錯(cuò)誤.
故選:C.
4.若將函數(shù)y=2x2的圖象向右平行移動(dòng)1個(gè)單位,再向上平移5個(gè)單位,可得到的拋物線是( )
A.y=2(x﹣1)2﹣5B.y=2(x﹣1)2+5C.y=2(x+1)2﹣5D.y=2(x+1)2+5
【考點(diǎn)】二次函數(shù)圖象與幾何變換.
【分析】拋物線平移不改變a的值.
【解答】解:原拋物線的頂點(diǎn)為(0,0),向右平行移動(dòng)1個(gè)單位,再向上平移5個(gè)單位,那么新拋物線的頂點(diǎn)為(1,5).可設(shè)新拋物線的解析式為y=2(x﹣h)2+k,代入人得:y=2(x﹣1)2﹣5.
故選B.
5.雙曲線y=![]() (k≠0)經(jīng)過(1,﹣4),下列各點(diǎn)在此雙曲線上的是( )
(k≠0)經(jīng)過(1,﹣4),下列各點(diǎn)在此雙曲線上的是( )
A.(﹣1,﹣4)B.(4,1)C.(﹣2,﹣2)D.(![]() ,﹣4
,﹣4![]() )
)
【考點(diǎn)】反比例函數(shù)圖象上點(diǎn)的坐標(biāo)特征.
【分析】將(1,﹣4)代入y=![]() 即可求出k的值,再根據(jù)k=xy解答即可.
即可求出k的值,再根據(jù)k=xy解答即可.
【解答】解:∵雙曲線y=![]() (k≠0)經(jīng)過(1,﹣4),
(k≠0)經(jīng)過(1,﹣4),
∴k=1×(﹣4)=﹣4
四個(gè)選項(xiàng)中只有D![]() =﹣4符合,
=﹣4符合,
故選:D.
6.如圖,點(diǎn)A、B、C是⊙O上的點(diǎn),若∠ACB=35°,則∠AOB的度數(shù)為( )
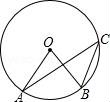
A.35°B.70°C.105°D.150°
【考點(diǎn)】圓周角定理.
【分析】在同圓或等圓中,同弧或等弧所對(duì)的圓周角相等,都等于這條弧所對(duì)的圓心角的一半.
【解答】解:由圓周角定理可得:∠AOB=2∠ACB=70°.
故選B.
7.如圖,為了測(cè)量河兩岸A、B兩點(diǎn)的距離,在與AB垂直的方向點(diǎn)C處測(cè)得AC=a,∠ACB=α,那么AB等于( )

A.a(chǎn)?sinαB.a(chǎn)?tanαC.a(chǎn)?cosαD.![]()
【考點(diǎn)】解直角三角形的應(yīng)用﹣方向角問題.
【分析】根據(jù)題意,可得Rt△ABC,同時(shí)可知AC與∠ACB.根據(jù)三角函數(shù)的定義解答.
【解答】解:根據(jù)題意,在Rt△ABC,有AC=a,∠ACB=α,且tanα=![]() ,
,
則AB=AC×tanα=a?tanα,
故選B.
8.如圖,△ABC中,∠ACB=70°,將△ABC繞點(diǎn)B按逆時(shí)針方向旋轉(zhuǎn)得到△BDE(點(diǎn)D與點(diǎn)A是對(duì)應(yīng)點(diǎn),點(diǎn)E與點(diǎn)C是對(duì)應(yīng)點(diǎn)),且邊DE恰好經(jīng)過點(diǎn)C,則∠ABD的度數(shù)為( )
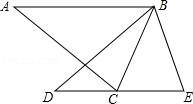
A.30°B.40°C.45°D.50°
【考點(diǎn)】旋轉(zhuǎn)的性質(zhì).
【分析】先根據(jù)旋轉(zhuǎn)的性質(zhì)得∠ABD=∠CBE,∠E=∠ACB=70°,BC=BE,則根據(jù)等腰三角形的性質(zhì)得∠BCE=∠E=70°,再利用三角形內(nèi)角和計(jì)算出∠CBE,從而得到∠ABD的度數(shù).
【解答】解:∵△ABC繞點(diǎn)B按逆時(shí)針方向旋轉(zhuǎn)得到△BDE(點(diǎn)D與點(diǎn)A是對(duì)應(yīng)點(diǎn),點(diǎn)E與點(diǎn)C是對(duì)應(yīng)點(diǎn)),
∴∠ABD=∠CBE,∠E=∠ACB=70°,BC=BE,
∴∠BCE=∠E=70°,
∴∠CBE=180°﹣70°﹣70°=40°,
∴∠ABD=40°.
故選B.
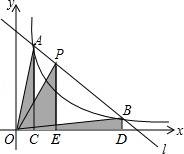
9.如圖,直線l和雙曲線![]() (k>0)交于A、B兩點(diǎn),P是線段AB上的點(diǎn)(不與A、B重合),過點(diǎn)A、B、P分別向x軸作垂線,垂足分別是C、D、E,連接OA、OB、OP,設(shè)△AOC面積是S1,△BOD面積是S2,△POE面積是S3,則( )
(k>0)交于A、B兩點(diǎn),P是線段AB上的點(diǎn)(不與A、B重合),過點(diǎn)A、B、P分別向x軸作垂線,垂足分別是C、D、E,連接OA、OB、OP,設(shè)△AOC面積是S1,△BOD面積是S2,△POE面積是S3,則( )
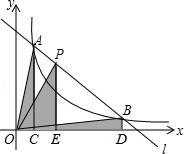
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
【考點(diǎn)】反比例函數(shù)系數(shù)k的幾何意義.
【分析】由于點(diǎn)A在y=![]() 上,可知S△AOC=
上,可知S△AOC=![]() k,又由于點(diǎn)P在雙曲線的上方,可知S△POE>
k,又由于點(diǎn)P在雙曲線的上方,可知S△POE>![]() k,而點(diǎn)B在y=
k,而點(diǎn)B在y=![]() 上,可知S△BOD=
上,可知S△BOD=![]() k,進(jìn)而可比較三個(gè)三角形面積的大小
k,進(jìn)而可比較三個(gè)三角形面積的大小
【解答】解:如右圖,
∵點(diǎn)A在y=![]() 上,
上,
∴S△AOC=![]() k,
k,
∵點(diǎn)P在雙曲線的上方,
∴S△POE>![]() k,
k,
∵點(diǎn)B在y=![]() 上,
上,
∴S△BOD=![]() k,
k,
∴S1=S2<S3.
故選;D.
10.某油箱容量為60L的汽車,加滿汽油后行駛了100km時(shí),油箱中的汽油大約消耗了![]() ,如果加滿汽油后汽車行駛的路程為xkm,油箱中剩油量為yL,則y與x之間的函數(shù)解析式和自變量取值范圍分別是( )
,如果加滿汽油后汽車行駛的路程為xkm,油箱中剩油量為yL,則y與x之間的函數(shù)解析式和自變量取值范圍分別是( )
A.y=0.12x,x>0B.y=60﹣0.12x,x>0
C.y=0.12x,0≤x≤500D.y=60﹣0.12x,0≤x≤500
【考點(diǎn)】根據(jù)實(shí)際問題列一次函數(shù)關(guān)系式.
【分析】根據(jù)題意列出一次函數(shù)解析式,即可求得答案.
【解答】解:因?yàn)橛拖淙萘繛?0L的汽車,加滿汽油后行駛了100km時(shí),油箱中的汽油大約消耗了![]() ,
,
可得:![]() L/km,60÷0.12=500(km),
L/km,60÷0.12=500(km),
所以y與x之間的函數(shù)解析式和自變量取值范圍是:y=60﹣0.12x,(0≤x≤500),
故選D.
二、填空題:(每題3分,共30分)
11.在Rt△ABC中,∠C=90°,AC=4,AB=5,則sinB的值是 ![]() .
.
【考點(diǎn)】銳角三角函數(shù)的定義.
【分析】根據(jù)正弦的定義計(jì)算即可.
【解答】解:∵∠C=90°,AC=4,AB=5,
∴sinB=![]() =
=![]() ,
,
故答案為:![]() .
.
12.計(jì)算:![]() +
+![]() ﹣3
﹣3![]() = 3
= 3![]() .
.
【考點(diǎn)】二次根式的加減法.
【分析】首先把二次根式化成最簡(jiǎn)二次根式,然后再合并即可.
【解答】解:原式=4![]() +2
+2![]() ﹣3
﹣3![]() =3
=3![]() ,
,
故答案為:3![]() .
.
13.把多項(xiàng)式2x2y﹣8xy2+8y3分解因式的結(jié)果是 2y(x﹣2y)2 .
【考點(diǎn)】提公因式法與公式法的綜合運(yùn)用.
【分析】根據(jù)提公因式法,可得完全平方公式,根據(jù)完全平方公式,可得答案.
【解答】解:原式=2y(x2﹣4xy+4y2)
=2y(x﹣2y)2,
故答案為:2y(x﹣2y)2.
14.不等式組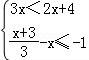 的解集是 3≤x<4 .
的解集是 3≤x<4 .
【考點(diǎn)】解一元一次不等式組.
【分析】分別求出不等式組中兩不等式的解集,找出解集的公共部分即可.
【解答】解: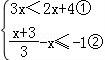 ,
,
由①得:x<4;
由②得:x≥3,
則不等式組的解集為3≤x<4.
故答案為:3≤x<4
15.已知二次函數(shù)y=﹣x2+mx+2的對(duì)稱軸為直線x=![]() ,則m=
,則m= ![]() .
.
【考點(diǎn)】二次函數(shù)的性質(zhì).
【分析】把二次函數(shù)解析式化為頂點(diǎn)式可用m表示出其對(duì)稱軸,再由條件可得到關(guān)于m的方程,可求得m的值.
【解答】解:∵y=﹣x2+mx+2=﹣(x﹣![]() )2+
)2+![]() +2,
+2,
∴二次函數(shù)對(duì)稱軸為直線x=![]() ,
,
∵二次函數(shù)的對(duì)稱軸為直線x=![]() ,
,
∴![]() =
=![]() ,解得m=
,解得m=![]() ,
,
故答案為:![]() .
.
16.已知扇形的圓心角為45°,弧長(zhǎng)為3π,則此扇形的半徑為 12 .
【考點(diǎn)】弧長(zhǎng)的計(jì)算.
【分析】根據(jù)弧長(zhǎng)公式l=![]() 代入求解即可.
代入求解即可.
【解答】解:∵l=![]() ,
,
∴r=![]() =12.
=12.
故答案為12.
17.如圖,△ABC內(nèi)接于⊙O,∠BAC=120°,AB=AC,BD為⊙O的直徑,AD=6,則BC= 6 .

【考點(diǎn)】圓周角定理;解直角三角形.
【分析】由已知可證∠BDA=30°;根據(jù)BD為⊙O的直徑,可證∠BAD=90°,得∠DBC=30°,即∠DBA=60°,所以BC=AD=6.
【解答】解:連接CD.
∵△ABC內(nèi)接于⊙O,∠BAC=120°,AB=AC,
∴∠CBA=∠BCA=30°.
∴∠BDA=∠ACB=30°.
∵BD為⊙O的直徑,
∴∠BAD=90°,∠BDA=30°,
∴∠DBC=90°﹣30°﹣30°=30°,
∴∠DBA=60°,∠BDC=60°,
∴BC=AD=6.
18.點(diǎn)A是反比例函數(shù)y=![]() 第二象限內(nèi)圖象上一點(diǎn),它到原點(diǎn)的距離為10,到x軸的距離為8,則k= ±48 .
第二象限內(nèi)圖象上一點(diǎn),它到原點(diǎn)的距離為10,到x軸的距離為8,則k= ±48 .
【考點(diǎn)】反比例函數(shù)圖象上點(diǎn)的坐標(biāo)特征.
【分析】由題意點(diǎn)A是反比例函數(shù)圖象上一點(diǎn),它到原點(diǎn)的距離為10,到x軸的距離為8,根據(jù)勾股定理可得其道y軸的距離為6,用待定系數(shù)法求出函數(shù)的表達(dá)式.
【解答】解:設(shè)反比例函數(shù)的解析式為:y=![]() ,
,
設(shè)A點(diǎn)為(a,b),
∵點(diǎn)A是反比例函數(shù)圖象上一點(diǎn),它到原點(diǎn)的距離為10,
∴a2+b2=100①,
∵點(diǎn)A到x軸的距離為8,
∴|b|=8,把b值代入①得,
∴|a|=6,
∴A(6,8)或(﹣6,﹣8)或(﹣6,8)或(6,﹣8),
把A點(diǎn)代入函數(shù)解析式y(tǒng)=![]() ,
,
得k=±48,
故答案為:±48.
19.已知:正方形ABCD的邊長(zhǎng)為2,點(diǎn)P是直線CD上一點(diǎn),若DP=1,則tan∠BPC的值是 2或![]() .
.
【考點(diǎn)】銳角三角函數(shù)的定義;勾股定理;正方形的性質(zhì).
【分析】本題可以利用銳角三角函數(shù)的定義、勾股定理以及正方形的性質(zhì)求解.
【解答】解:此題有兩種可能:
(1)∵BC=2,DP=1,
∠C=90°,
∴tan∠BPC=![]() =2;
=2;
(2)∵DP=1,DC=2,
∴PC=3,
又∵BC=2,∠C=90°,
∴tan∠BPC=![]() =
=![]() .
.
故答案為:2或![]() .
.
20.如圖,四邊形ABCD中,對(duì)角線AC⊥BD于點(diǎn)O,且AO=BO=4,CO=8,∠ADB=2∠ACB,則四邊形ABCD的面積為 42 .
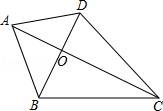
【考點(diǎn)】相似三角形的判定與性質(zhì).
【分析】如圖,作∠ADO的平分線DP交AC于P,作PE⊥AD于E.由△POD∽△BOC,得![]() =
=![]() ,設(shè)OP=x,推出OD=2x,由PE⊥AD,PO⊥DO,∠PDE=∠PDO,推出PE=OP,由
,設(shè)OP=x,推出OD=2x,由PE⊥AD,PO⊥DO,∠PDE=∠PDO,推出PE=OP,由![]() =
=![]() =
=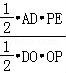 ,推出
,推出![]() =
=![]() ,推出AD=2(4﹣x),在Rt△ADO中,根據(jù)AD2=AO2+DO2,可得4(4﹣x)2=4x2+42,求出x的值,再根據(jù)S四邊形ABCD=S△ABD+S△BDC=
,推出AD=2(4﹣x),在Rt△ADO中,根據(jù)AD2=AO2+DO2,可得4(4﹣x)2=4x2+42,求出x的值,再根據(jù)S四邊形ABCD=S△ABD+S△BDC=![]() ?BD?AO+
?BD?AO+![]() ?BD?OC=
?BD?OC=![]() ?BD(OA+OC)計(jì)算即可.
?BD(OA+OC)計(jì)算即可.
【解答】解:如圖,作∠ADO的平分線DP交AC于P,作PE⊥AD于E.
∵∠ADO=2∠BCO,
∴∠PDO=∠BCO,
∵∠POD=∠BOC,
∴△POD∽△BOC,
∴![]() =
=![]() ,設(shè)OP=x,
,設(shè)OP=x,
∴![]() =
=![]() ,
,
∴OD=2x,
∵PE⊥AD,PO⊥DO,∠PDE=∠PDO,
∴PE=OP,
∴![]() =
=![]() =
=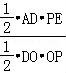 ,
,
∴![]() =
=![]() ,
,
∴AD=2(4﹣x),
在Rt△ADO中,∵AD2=AO2+DO2,
∴4(4﹣x)2=4x2+42,
∴x=![]() ,
,
∴OD=3,
∴S四邊形ABCD=S△ABD+S△BDC=![]() ?BD?AO+
?BD?AO+![]() ?BD?OC=
?BD?OC=![]() ?BD(OA+OC)=
?BD(OA+OC)=![]() ×7×12=42.
×7×12=42.
故答案為42.
三、解答題:(21、22題7分,23題、24題8分,25-27題各10分)
21.先化簡(jiǎn),再求代數(shù)式的值:![]() ,其中a=tan60°﹣2sin30°.
,其中a=tan60°﹣2sin30°.
【考點(diǎn)】分式的化簡(jiǎn)求值;特殊角的三角函數(shù)值.
【分析】分別化簡(jiǎn)分式和a的值,再代入計(jì)算求值.
【解答】解:原式=![]() .
.
當(dāng)a=tan60°﹣2sin30°=![]() ﹣2×
﹣2×![]() =
=![]() 時(shí),
時(shí),
原式=![]() .
.
22.如圖,在小正方形的邊長(zhǎng)均為1的方格紙中,有線段AB,點(diǎn)A、B均在小正方形的頂點(diǎn)上.
(1)在圖1中畫一個(gè)以線段AB為一邊的平行四邊形ABCD,點(diǎn)C、D均在小正方形的頂點(diǎn)上,且平行四邊形ABCD的面積為10;
(2)在圖2中畫一個(gè)鈍角三角形ABE,點(diǎn)E在小正方形的頂點(diǎn)上,且三角形ABE的面積為4,tan∠AEB=![]() .請(qǐng)直接寫出BE的長(zhǎng).
.請(qǐng)直接寫出BE的長(zhǎng).
【考點(diǎn)】作圖—應(yīng)用與設(shè)計(jì)作圖;勾股定理;平行四邊形的判定;解直角三角形.
【分析】(1)由圖可知A、B間的垂直方向長(zhǎng)為2,要使構(gòu)建平行四邊形ABCD的面積為10,則可以在A的水平方向取一條長(zhǎng)為5的線段,可得點(diǎn)C;
(2)由圖可知A、B間的垂直方向長(zhǎng)為2,要使構(gòu)建的鈍角三角形ABE面積為4,則可以在A的水平方向取一條長(zhǎng)為4的線段,可得點(diǎn)E,且tan∠AEB=![]() ,BE的長(zhǎng)可以根據(jù)勾股定理求得.
,BE的長(zhǎng)可以根據(jù)勾股定理求得.
【解答】解:(1)如圖1所示;
(2)如圖2所示;

BE=![]() =2
=2![]() .
.
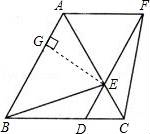
23.如圖,已知△ABC是等邊三角形,D、E分別在邊BC、AC上,且CD=CE,連接DE并延長(zhǎng)至點(diǎn)F,使EF=AE,連接AF、BE和CF.
(1)判斷四邊形ABDF是怎樣的四邊形,并說明理由;
(2)若AB=6,BD=2DC,求四邊形ABEF的面積.

【考點(diǎn)】平行四邊形的判定與性質(zhì);等邊三角形的判定與性質(zhì);勾股定理.
【分析】(1)等邊三角形的三邊相等,三個(gè)角也相等,根據(jù)等邊三角形的性質(zhì)能證明AF∥BD,AB∥FD,所以四邊形ABDF是怎樣的四邊形.
(2)過點(diǎn)E作EG⊥AB于點(diǎn)G,可求出EG的長(zhǎng),面積可求.
【解答】解:(1)∵CD=CE,∠BCA=60°,
∴△DEC是等邊三角形,
∴∠DEC=∠EDC=∠AEF=60°,
∵△ABC是等邊三角形,
∴∠ABC=60°,
∴AB∥DF,
∵EF=AE,∠AEF=60°,
∴△AEF是等邊三角形,
∴∠AFD=60°,
∴BD∥AF,
∴四邊形ABDF是平行四邊形;
(2)∵四邊形ABDF是平行四邊形,
∴EF∥AB,且EF≠AB,
∴四邊形ABEF是梯形.
過點(diǎn)E作EG⊥AB于點(diǎn)G,
∵BD=2DC,AB=6,
∴AE=BD=EF=4,
∵∠AGE=90°,∠BAC=60°,
∴∠AEG=30°,
∴AG=![]() AE=2,
AE=2,
EG=![]() =
=![]() =2
=2![]() ,
,
∴S=![]() (4+6)×2
(4+6)×2![]() =10
=10![]() .
.
24.如圖,在平面直角坐標(biāo)系中,點(diǎn)O為坐標(biāo)原點(diǎn),△OAB的頂點(diǎn)B在x軸負(fù)半軸上,OA=OB=5,tan∠AOB=![]() ,點(diǎn)P與點(diǎn)A關(guān)于y軸對(duì)稱,點(diǎn)P在反比例函數(shù)y=
,點(diǎn)P與點(diǎn)A關(guān)于y軸對(duì)稱,點(diǎn)P在反比例函數(shù)y=![]() 的圖象上.
的圖象上.
(1)求反比例函數(shù)的解析式;
(2)點(diǎn)D在反比例函數(shù)y=![]() 第一象限的圖象上,且△APD的面積為4,求點(diǎn)D的坐標(biāo).
第一象限的圖象上,且△APD的面積為4,求點(diǎn)D的坐標(biāo).
【考點(diǎn)】待定系數(shù)法求反比例函數(shù)解析式;反比例函數(shù)系數(shù)k的幾何意義;等腰三角形的性質(zhì);解直角三角形.
【分析】(1)首先過點(diǎn)A作AC⊥x軸,由線段OA=5,點(diǎn)B在x軸負(fù)半軸上,且tan∠AOB=![]() ,可求得點(diǎn)A的坐標(biāo),進(jìn)而求得P的坐標(biāo),然后利用待定系數(shù)法求得反比例函數(shù)的解析式;
,可求得點(diǎn)A的坐標(biāo),進(jìn)而求得P的坐標(biāo),然后利用待定系數(shù)法求得反比例函數(shù)的解析式;
(2)根據(jù)三角形面積求得D的縱坐標(biāo),代入反比例函數(shù)式,即可求得橫坐標(biāo).
【解答】解:(1)過點(diǎn)A作AC⊥x軸,
∵在Rt△AOC中,tan∠AOB=![]() =
=![]() ,
,
設(shè)AC=3x,OC=4x,
∵OA=5,
在Rt△AOD中,根據(jù)勾股定理解得AC=3,OC=4,
∴A(﹣4,3),
∵點(diǎn)P與點(diǎn)A關(guān)于y軸對(duì)稱,
∴P(4,3),
把P(4,3)代入反比例函數(shù)y=![]() 中,
中,
解得:k=12,
則反比例函數(shù)的解析式為y=![]() ;
;
(2)∵A(﹣4,3),P(4,3),
∴AP=8,
∵△APD的面積為4,
∴D的縱坐標(biāo)為4或2,
把y=4代入y=![]() 求得,x=3,
求得,x=3,
把y=2代入y=![]() 求得,x=6,
求得,x=6,
∴D的坐標(biāo)為(3,4)或(6,2).
25.工藝商場(chǎng)按標(biāo)價(jià)銷售某種工藝品時(shí),每件可獲利45元;按標(biāo)價(jià)的八五折銷售該工藝品8件與將標(biāo)價(jià)降低35元銷售該工藝品12件所獲利潤(rùn)相等.
(1)該工藝品每件的進(jìn)價(jià)、標(biāo)價(jià)分別是多少元?
(2)若每件工藝品按(1)中求得的進(jìn)價(jià)進(jìn)貨,標(biāo)價(jià)售出,工藝商場(chǎng)每天可售出該工藝品100件.若每件工藝品降價(jià)1元,則每天可多售出該工藝品4件.問每件工藝品降價(jià)多少元出售,每天獲得的利潤(rùn)最大?獲得的最大利潤(rùn)是多少元?
【考點(diǎn)】二次函數(shù)的應(yīng)用;二元一次方程組的應(yīng)用.
【分析】(1)根據(jù)“每件獲利45元”可得出:每件標(biāo)價(jià)﹣每件進(jìn)價(jià)=45元;根據(jù)“標(biāo)價(jià)的八五折銷售該工藝品8件與將標(biāo)價(jià)降低35元銷售該工藝品12件所獲利潤(rùn)相等”可得出等量關(guān)系:每件標(biāo)價(jià)的八五折×8﹣每件進(jìn)價(jià)×8=(每件標(biāo)價(jià)﹣35元)×12﹣每件進(jìn)價(jià)×12.
(2)可根據(jù)題意列出關(guān)于總利潤(rùn)和每天利潤(rùn)的二次函數(shù),以此求出問題.
【解答】解:(1)設(shè)該工藝品每件的進(jìn)價(jià)是x元,標(biāo)價(jià)是y元.
依題意得方程組:
![]()
解得:![]() .
.
故該工藝品每件的進(jìn)價(jià)是155元,標(biāo)價(jià)是200元.
(2)設(shè)每件應(yīng)降價(jià)a元出售,每天獲得的利潤(rùn)為W元.
依題意可得W與a的函數(shù)關(guān)系式:W=(45﹣a),
W=﹣4a2+80a+4500,
配方得:W=﹣4(a﹣10)2+4900,
當(dāng)a=10時(shí),W最大=4900.
故每件應(yīng)降價(jià)10元出售,每天獲得的利潤(rùn)最大,最大利潤(rùn)是4900元.
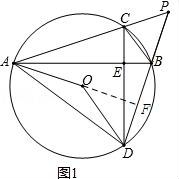
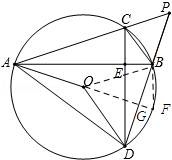
26.如圖,⊙O中弦AB⊥弦CD于E,延長(zhǎng)AC、DB交于點(diǎn)P,連接AO、DO、AD、BC.
(1)求證:∠AOD=90°+∠P;
(2)若AB平分∠CAO,求證:AD=AB;
(3)在(2)的條件下,若⊙O的半徑為5,PB=![]() ,求弦BC的長(zhǎng).
,求弦BC的長(zhǎng).

【考點(diǎn)】圓的綜合題.
【分析】(1)由圓周角定理可知∠AOD=2∠ACD,結(jié)合三角形的外角的性質(zhì)可得到∠AOD=2∠CDP+2∠P,接下來,依據(jù)∠CAE=∠CDP,可將∠AOD轉(zhuǎn)化為∠CDP、∠CAE、2∠P,最后根據(jù)∠CAE+∠CDP+∠P=90°可證得問題的答案;
(2)延長(zhǎng)AO交BD與點(diǎn)F.首先證明∠AFB=∠AEC=90°,接下來,再證明△AFD≌△ADB,由全等三角形的性質(zhì)可得到AB=AD;
(3)延長(zhǎng)AO交BD與點(diǎn)G交⊙O與點(diǎn)F,連結(jié)BF、OB.依據(jù)弧、弦、弦心距之間的關(guān)系可知BC=FB,接下來,證明OB∥AP,依據(jù)平行線分線段成比例定理可知![]() ,故此可得到
,故此可得到![]() =
=![]() ,在△OBG中由勾股定理可得到OG=4,BG=3,從而可求得GF=1,在Rt△BGF中,由勾股定理得可求得BF的長(zhǎng),于是得到BC的長(zhǎng).
,在△OBG中由勾股定理可得到OG=4,BG=3,從而可求得GF=1,在Rt△BGF中,由勾股定理得可求得BF的長(zhǎng),于是得到BC的長(zhǎng).
【解答】解:(1)∵∠CDP+∠P=∠ACD,∠AOD=2∠ACD,
∴∠AOD=2∠CDP+2∠P.
∵∠CAE=∠CDP,
∴∠AOD=∠CDP+∠CAE+∠P+∠P
∵AB⊥CD,
∴∠CAE+∠ACD=90°.
∴∠CAE+∠CDP+∠P=90°.
∴∠AOD=90°+∠P.
(2)如圖1所示:延長(zhǎng)AO交BD與點(diǎn)F.
∵AB平分∠CAO,
∴∠CAE=∠BAF.
又∵∠ACE=∠ABF,
∴△ACE∽△ABF.
∴∠AFB=∠AEC=90°.
∴AF⊥BD.
∴FD=BF.
在△ABF和△ADF中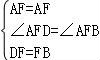 ,
,
∴△AFD≌△ADB.
∴AB=AD.
(3)延長(zhǎng)AO交BD與點(diǎn)G交⊙O與點(diǎn)F,連結(jié)BF、OB.
∵∠CAB=∠OAB,
∴![]() .
.
∴BC=FB.
∵OA=OB,
∴∠OAB=∠OBA.
∴∠CAB=∠OBA.
∴OB∥AP.
∴![]() .
.
∴![]() =
=![]() .
.
設(shè)OG=4k,GB=3k.
在△OBG中,由勾股定理可知:(4k)2+(3k)2=25.
解得:k=1(負(fù)值已舍去).
∴OG=4,BG=3.
∴GF=1.
在Rt△BGF中,由勾股定理得:BF=![]() =
=![]() .
.
∴BC=![]() .
.
27.如圖所示,平面直角坐標(biāo)系中,O為原點(diǎn),拋物線y=﹣x2+2k(k≠0)頂點(diǎn)為C點(diǎn),拋物線交x軸于A、B兩點(diǎn),且AB=CO;
(1)求此拋物線解析式;
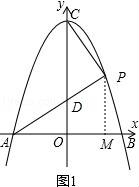
(2)點(diǎn)P為第一象限內(nèi)拋物線上一點(diǎn),連接PA交y軸于點(diǎn)D,連接PC,設(shè)點(diǎn)P的橫坐標(biāo)為t,△PCD的面積為S,求S與t的函數(shù)關(guān)系式,并直接寫出t的取值范圍;
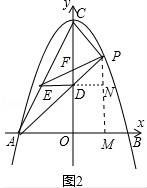
(3)在(2)的條件下,連接AC,過點(diǎn)D作DE⊥y軸交AC于E,連接PE,交y軸于F,若5CF=3OF,求P點(diǎn)坐標(biāo).
【考點(diǎn)】二次函數(shù)綜合題.
【分析】(1)由題意點(diǎn)B坐標(biāo)(k,0),代入拋物線y=﹣x2+2k得﹣k2+2k=0,解方程即可.
(2)如圖1中,作PM⊥AB于M.設(shè)點(diǎn)P坐標(biāo)(t,﹣t2+4),由OD∥PM,得![]() =
=![]() ,求出OD,即可解決問題.
,求出OD,即可解決問題.
(3))如圖2中,作PM⊥AB于M,ED的延長(zhǎng)線交PM于N.先求出直線AC解析式,得到點(diǎn)E坐標(biāo),推出DE=DN,推出DF是△EPN的中位線,根據(jù)PN=2DF,列出方程即可解決問題.
【解答】解:(1)∵拋物線y=﹣x2+2k(k≠0)頂點(diǎn)為C點(diǎn),
∴點(diǎn)C坐標(biāo)(0,2k,
∵AB=CO,OA=OB,
∴點(diǎn)B坐標(biāo)(k,0),代入拋物線y=﹣x2+2k得﹣k2+2k=0,
∴k=2或0(舍棄),
∴拋物線解析式為y=﹣x2+4.
(2)如圖1中,作PM⊥AB于M.
設(shè)點(diǎn)P坐標(biāo)(t,﹣t2+4),
∵OD∥PM,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴OD=4﹣2t,
∴CD=4﹣(4﹣2t)=2t,
∴S=![]() ?2t?t=t2,(0<t<2)
?2t?t=t2,(0<t<2)
(3)如圖2中,作PM⊥AB于M,ED的延長(zhǎng)線交PM于N.
∵∠NDO=∠DOM=∠NMO=90°,
∴四邊形OMND是矩形,
∴DN=OM=t
∵OC=4,5CF=3OF,設(shè)CF=3k,OF=5k,
則8k=4,
∴k=![]() ,
,
∴CF=![]() ,OF=
,OF=![]() ,
,
∵直線AC的解析式為y=2x+4,D(0,4﹣2t),DE⊥OC,
∴E(﹣t,4﹣2t),
∴ED=DN=OM=t
∵DF∥PN,
∴EF=FP,
∴PN=2DF,
∴﹣t2+4﹣(4﹣2t)=2[![]() ﹣(4﹣2t)],
﹣(4﹣2t)],
∴t2+2t﹣3=0,
∴t=1或﹣3(舍棄),
∴點(diǎn)P坐標(biāo)(1,3).
2017年3月16日

孔乙己是貧困潦倒的知識(shí)分子。在書中,孔乙己是一個(gè)知識(shí)分子,滿口“之乎者也”,但是他很窮,還竊書,說過“讀書人的事,怎么能叫竊,”被人嘲笑,他...

自然界產(chǎn)生氧氣的化學(xué)方程式:光合作用的反應(yīng)式為6CO2+12H2O→C6H12O6+6O2+6H2O。包括光反應(yīng)和暗反應(yīng)兩個(gè)過程。需要具備光...

有的高校沒有條件,只要學(xué)業(yè)水平成績(jī)都合格就可以,比如中國科學(xué)院大學(xué)。有的需要平常學(xué)習(xí)考試成績(jī),比如北京外國語大學(xué)要求高三第一學(xué)期期末成績(jī)?cè)谌?..

在四則運(yùn)算中,表示計(jì)算順序,在小括號(hào)之后、大括號(hào)之前;表示兩個(gè)整數(shù)的最小公倍數(shù);表示取未知數(shù)的整數(shù)部分;在函數(shù)中,表示函數(shù)的閉區(qū)間;在線性代...

濟(jì)南開設(shè)的最好的職高學(xué)校有:濟(jì)南方信集團(tuán)職業(yè)高中、濟(jì)南公共交通職業(yè)高中。濟(jì)南市公共交通職業(yè)高級(jí)中學(xué)是由濟(jì)南市公共交通總公司承辦,業(yè)務(wù)屬濟(jì)南市...

實(shí)然:是說事物實(shí)際上就是這樣的,但不同于現(xiàn)實(shí)性(現(xiàn)實(shí)性指其有合理性和客觀性);應(yīng)然:就是應(yīng)該是怎么樣的意思,比如說這件事,就應(yīng)該是那樣的結(jié)果...

地中海氣候一種夏季炎熱干燥、冬季溫和多雨,雨熱不同期的氣候類型。地中海氣候冬季受西風(fēng)帶控制,鋒面氣旋頻繁活動(dòng),氣候溫和,最冷月的氣溫在4-1...

堿石灰,又稱鈉石灰,堿石灰是白色或米黃色粉末,疏松多孔,是氧化鈣(CaO,大約75%),水(H?O,大約20%),氫氧化鈉(NaOH,大約3...