2017湛江市徐聞縣九年級數學模擬試題【解析版含答案】

由于版式的問題，試題可能會出現亂碼的現象，為了方便您的閱讀請點擊全屏查看一、選擇題：本大題共10小題，每小題3分，共30分，在每小題給出的四個選項中，只有一個是正確的．

1．方程3x2﹣1=0的一次項系數是（）

A．﹣1????????????? B．0????????????? C．3????????????? D．1

2．方程x（x﹣1）=0的根是（）

A．x=0????????????? B．x=1????????????? C．x1=0，x2=1????????????? D．x1=0，x2=﹣1

3．拋物線y=2（x+1）2﹣3的對稱軸是（）

A．直線x=1????????????? B．直線x=3????????????? C．直線x=﹣1????????????? D．直線x=﹣3

4．下列所述圖形中，是中心對稱圖形的是（）

A．直角三角形????????????? B．平行四邊形????????????? C．正五邊形????????????? D．正三角形

5．用配方法解一元二次方程x2﹣6x﹣10=0時，下列變形正確的為（）

A．（x+3）2=1????????????? B．（x﹣3）2=1????????????? C．（x+3）2=19????????????? D．（x﹣3）2=19

6．如圖，在Rt△ABC中，∠ACB=90°，∠ABC=30°，將△ABC繞點C順時針旋轉至△A′B′C，使點A′恰好落在AB上，則旋轉角度為（）

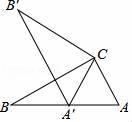
A．30°????????????? B．45°????????????? C．60°????????????? D．90°

7．若關于x的方程x2+x﹣a+=0有兩個不相等的實數根，則實數a的取值范圍是（）

A．a＞2????????????? B．a≥2????????????? C．a≤2????????????? D．a＜2

8．三角形兩邊的長是3和4，第三邊的長是方程x2﹣12x+35=0的根，則該三角形的周長為（）

A．14????????????? B．12????????????? C．12或14????????????? D．以上都不對

9．設二次函數y=（x﹣3）2﹣4圖象的對稱軸為直線l，若點M在直線l上，則點M的坐標可能是（）

A．（1，0）????????????? B．（3，0）????????????? C．（﹣3，0）????????????? D．（0，﹣4）

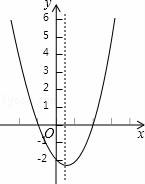
10．二次函數y=ax2+bx+c（a≠0）的大致圖象如圖，關于該二次函數，下列說法錯誤的是（）

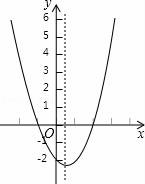
A．函數有最小值????????????? B．對稱軸是直線x=

C．當x＜，y隨x的增大而減小????????????? D．當﹣1＜x＜2時，y＞0

二、填空題：本大題共6小題，每小題4分，共24分．

11．把方程2x2﹣1=5x化為一般形式是．

12．點P（﹣1，2）關于原點對稱的點P′的坐標是．

13．若x=﹣1是一元二次方程x2+2x+a=0的一個根，那么a=．

14．請寫出一個開口向上，且其圖象經過原點的拋物線的解析式．

15．已知點A（，y1），B（﹣2，y2）都在二次函數y=（x﹣2）2﹣1的圖象上，則y1與y2的大小關系是．

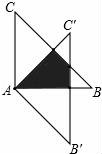
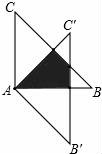
16．如圖，△ABC繞點A順時針旋轉45°得到△AB′C′，若∠BAC=90°，AB=AC=，則圖中陰影部分的面積等于．

三、解答題（一）：本大題共3小題，每小題6分，共18分．

17．（6分）解方程：x2﹣3x+2=0．

18．（6分）已知二次函數y=﹣x2﹣2x，用配方法把該函數化為y=a（x﹣h）2+c的形式，并指出函數圖象的對稱軸和頂點坐標．

19．（6分）已知x=1是關于x的一元二次方程x2+3x﹣m=0的一個根，求m的值和方程的另一個根．

四、解答題（二）：本大題3小題，每小題7分，共21分．

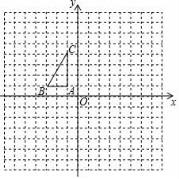
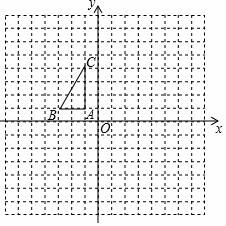
20．（7分）如圖，在平面直角坐標系中，已知△ABC的三個頂點的坐標分別為（﹣1，1），B（﹣3，1），C（﹣1，4）．

（1）將△ABC繞點A順時針旋轉90°后得到△AB′C′，請在圖中畫出△AB′C′．

（2）寫出點B′、C′的坐標．

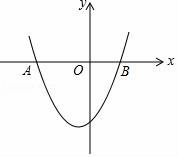
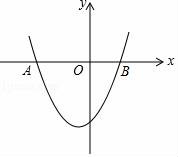
21．（7分）如圖，已知拋物線y=x2+x﹣6與x軸兩個交點分別是A、B（點A在點B的左側）．

（1）求A、B的坐標；

（2）利用函數圖象，寫出y＜0時，x的取值范圍．

22．（7分）向陽村2013年的人均收入為10000元，2015年人均收入為12100元，若2013年到2015年人均收入的年平均增長率相同．

（1）求人均收入的年平均增長率；

（2）2014年的人均收入是多少元？

五、解答題（三）：本大題3小題，每小題9分，共27分．

23．（9分）如圖所示，一個農戶要建一個矩形豬舍，豬舍的一邊利用長為12m的房墻，另外三邊用25m長的建筑材料圍成，為了方便進出，在垂直于房墻的一邊留一個1m寬的門．

（1）所圍成矩形豬舍的長、寬分別是多少時，豬舍面積為80m2？

（2）為做好豬舍的衛生防疫，現需要對圍成的矩形進行硬底化，若以房墻的長為矩形豬舍一邊的長，且已知硬底化的造價為60元/平方米，請你幫助農戶計算矩形豬舍硬底化需要的費用．

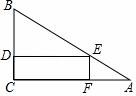
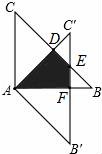
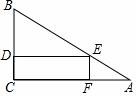
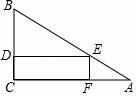
24．（9分）一塊三角形材料如圖所示，∠A=30°，∠C=90°，AB=12，用這塊材料剪出一個矩形CDEF，其中D、E、F分別在BC、AB、AC上．

（1）若設AE=x，則AF=；（用含x的代數式表示）

（2）要使剪出的矩形CDEF的面積最大，點E應選在何處？

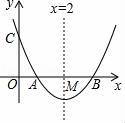
25．（9分）如圖，已知拋物線y=x2+bx+c與x軸交于點A、B，AB=2，與y軸交于點C，對稱軸為直線x=2，對稱軸交x軸于點M．

（1）求拋物線的函數解析式；

（2）設P為對稱軸上一動點，求△APC周長的最小值；

（3）設D為拋物線上一點，E為對稱軸上一點，若以點A、B、D、E為頂點的四邊形是菱形，則點D的坐標為．

2017湛江市徐聞縣九年級數學模擬試題參考答案與試題解析

一、選擇題：本大題共10小題，每小題3分，共30分，在每小題給出的四個選項中，只有一個是正確的．

1．方程3x2﹣1=0的一次項系數是（）

A．﹣1????????????? B．0????????????? C．3????????????? D．1

【考點】一元二次方程的一般形式．

【分析】根據一元二次方程的一般形式，可得答案．

【解答】解：3x2﹣1=0的一次項系數是0，

故選：B．

【點評】本題考查了一元二次方程的一般形式，熟記一元二次方程的一般形式是解題關鍵．

2．方程x（x﹣1）=0的根是（）

A．x=0????????????? B．x=1????????????? C．x1=0，x2=1????????????? D．x1=0，x2=﹣1

【考點】解一元二次方程-因式分解法．

【分析】由題意推出x=0，或（x﹣1）=0，解方程即可求出x的值．

【解答】解：∵x（x﹣1）=0，

∴x1=0，x2=1，

故選擇C．

【點評】本題主要考查解一元二次方程，關鍵在于根據題意推出x=0，或（x﹣1）=0即可．

3．拋物線y=2（x+1）2﹣3的對稱軸是（）

A．直線x=1????????????? B．直線x=3????????????? C．直線x=﹣1????????????? D．直線x=﹣3

【考點】二次函數的性質．

【分析】由拋物線解析式可求得答案．

【解答】解：

∵y=2（x+1）2﹣3，

∴對稱軸為直線x=﹣1，

故選C．

【點評】本題主要考查二次函數的性質，掌握二次函數的頂點式是解題的關鍵，即在y=a（x﹣h）2+k中，對稱軸為x=h，頂點坐標為（h，k）．

4．下列所述圖形中，是中心對稱圖形的是（）

A．直角三角形????????????? B．平行四邊形????????????? C．正五邊形????????????? D．正三角形

【考點】中心對稱圖形．

【分析】根據中心對稱圖形的定義對各選項分析判斷即可得解．

【解答】解：A、直角三角形不是中心對稱圖形，故本選項錯誤；

B、平行四邊形是中心對稱圖形，故本選項正確；

C、正五邊形不是中心對稱圖形，故本選項錯誤；

D、正三角形不是中心對稱圖形，故本選項錯誤．

故選B．

【點評】本題考查了中心對稱圖形的概念，中心對稱圖形是要尋找對稱中心，旋轉180度后兩部分重合．

5．用配方法解一元二次方程x2﹣6x﹣10=0時，下列變形正確的為（）

A．（x+3）2=1????????????? B．（x﹣3）2=1????????????? C．（x+3）2=19????????????? D．（x﹣3）2=19

【考點】解一元二次方程-配方法．

【分析】方程移項變形后，利用完全平方公式化簡得到結果，即可做出判斷．

【解答】解：方程移項得：x2﹣6x=10，

配方得：x2﹣6x+9=19，即（x﹣3）2=19，

故選D．

【點評】此題考查了解一元二次方程﹣配方法，熟練掌握完全平方公式是解本題的關鍵．

6．如圖，在Rt△ABC中，∠ACB=90°，∠ABC=30°，將△ABC繞點C順時針旋轉至△A′B′C，使點A′恰好落在AB上，則旋轉角度為（）

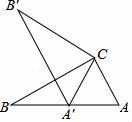
A．30°????????????? B．45°????????????? C．60°????????????? D．90°

【考點】旋轉的性質．

【分析】先利用互余得到∠A=60°，再根據旋轉的性質得CA′=CA，∠ACA′等于旋轉角，然后判斷△ACA′為等邊三角形得到∠ACA′=60°，從而得到旋轉角的度數．

【解答】解：∵∠ACB=90°，∠ABC=30°，

∴∠A=60°，

∵△ABC繞點C順時針旋轉至△A′B′C，使得點A′恰好落在AB上，

∴CA′=CA，∠ACA′等于旋轉角，

∴△ACA′為等邊三角形，

∴∠ACA′=60°，

即旋轉角度為60°．

故選C．

【點評】本題考查了旋轉的性質：對應點到旋轉中心的距離相等；對應點與旋轉中心所連線段的夾角等于旋轉角；旋轉前、后的圖形全等．本題的關鍵是證明△ACA′為等邊三角形．

7．若關于x的方程x2+x﹣a+=0有兩個不相等的實數根，則實數a的取值范圍是（）

A．a＞2????????????? B．a≥2????????????? C．a≤2????????????? D．a＜2

【考點】根的判別式．

【分析】根據判別式的意義得到△=12﹣4×（﹣a+）＞0，然后解不等式即可．

【解答】解：根據題意得△=12﹣4×（﹣a+）＞0，解得a＞2．

故選A．

【點評】本題考查了一元二次方程根的判別式：一元二次方程ax2+bx+c=0（a≠0）的根與△=b2﹣4ac有如下關系：當△＞0時，方程有兩個不相等的兩個實數根；當△=0時，方程有兩個相等的兩個實數根；當△＜0時，方程無實數根．

8．三角形兩邊的長是3和4，第三邊的長是方程x2﹣12x+35=0的根，則該三角形的周長為（）

A．14????????????? B．12????????????? C．12或14????????????? D．以上都不對

【考點】解一元二次方程-因式分解法；三角形三邊關系．

【分析】易得方程的兩根，那么根據三角形的三邊關系，排除不合題意的邊，進而求得三角形周長即可．

【解答】解：解方程x2﹣12x+35=0得：x=5或x=7．

當x=7時，3+4=7，不能組成三角形；

當x=5時，3+4＞5，三邊能夠組成三角形．

∴該三角形的周長為3+4+5=12，故選B．

【點評】本題主要考查三角形三邊關系，注意在求周長時一定要先判斷是否能構成三角形．

9．設二次函數y=（x﹣3）2﹣4圖象的對稱軸為直線l，若點M在直線l上，則點M的坐標可能是（）

A．（1，0）????????????? B．（3，0）????????????? C．（﹣3，0）????????????? D．（0，﹣4）

【考點】二次函數的性質．

【分析】根據二次函數的解析式可得出直線l的方程為x=3，點M在直線l上則點M的橫坐標一定為3，從而選出答案．

【解答】解：∵二次函數y=（x﹣3）2﹣4圖象的對稱軸為直線x=3，

∴直線l上所有點的橫坐標都是3，

∵點M在直線l上，

∴點M的橫坐標為3，

故選B．

【點評】本題考查了二次函數的性質，解答本題的關鍵是掌握二次函數y=a（x﹣h）2+k的頂點坐標為（h，k），對稱軸是x=h．

10．二次函數y=ax2+bx+c（a≠0）的大致圖象如圖，關于該二次函數，下列說法錯誤的是（）

A．函數有最小值????????????? B．對稱軸是直線x=

C．當x＜，y隨x的增大而減小????????????? D．當﹣1＜x＜2時，y＞0

【考點】二次函數的性質．

【分析】根據拋物線的開口方向，利用二次函數的性質判斷A；

根據圖形直接判斷B；

根據對稱軸結合開口方向得出函數的增減性，進而判斷C；

根據圖象，當﹣1＜x＜2時，拋物線落在x軸的下方，則y＜0，從而判斷D．

【解答】解：A、由拋物線的開口向上，可知a＞0，函數有最小值，正確，故A選項不符合題意；

B、由圖象可知，對稱軸為x=，正確，故B選項不符合題意；

C、因為a＞0，所以，當x＜時，y隨x的增大而減小，正確，故C選項不符合題意；

D、由圖象可知，當﹣1＜x＜2時，y＜0，錯誤，故D選項符合題意．

故選：D．

【點評】本題考查了二次函數的圖象和性質，解題的關鍵是利用數形結合思想解題．

二、填空題：本大題共6小題，每小題4分，共24分．

11．把方程2x2﹣1=5x化為一般形式是　2x2﹣5x﹣1=0　．

【考點】一元二次方程的一般形式．

【分析】一元二次方程ax2+bx+c=0（a，b，c是常數且a≠0）的a、b、c分別是二次項系數、一次項系數、常數項．

【解答】解：2x2﹣1=5x化為一般形式是2x2﹣5x﹣1=0，

故答案為：2x2﹣5x﹣1=0．

【點評】本題考查了一元二次方程的一般形式：ax2+bx+c=0（a，b，c是常數且a≠0）特別要注意a≠0的條件．這是在做題過程中容易忽視的知識點．在一般形式中ax2叫二次項，bx叫一次項，c是常數項．其中a，b，c分別叫二次項系數，一次項系數，常數項．

12．點P（﹣1，2）關于原點對稱的點P′的坐標是　（1，﹣2）　．

【考點】關于原點對稱的點的坐標．

【分析】根據關于原點對稱的點的橫坐標與縱坐標都互為相反數解答．

【解答】解：點P（﹣1，2）關于原點對稱的點P′的坐標是（1，﹣2）．

故答案為：（1，﹣2）．

【點評】本題考查了關于原點對稱的點的坐標，熟記關于原點對稱的點的橫坐標與縱坐標都互為相反數是解題的關鍵．

13．若x=﹣1是一元二次方程x2+2x+a=0的一個根，那么a=　1　．

【考點】一元二次方程的解．

【分析】根據方程的根的定義將x=﹣1代入方程得到關于a的方程，然后解得a的值即可．

【解答】解：將x=﹣1代入得：1﹣2+a=0，

解得：a=1．

故答案為：1．

【點評】本題主要考查的是方程的解（根）的定義和一元一次方程的解法，將方程的解代入方程是解題的關鍵．

14．請寫出一個開口向上，且其圖象經過原點的拋物線的解析式　y=x2+x　．

【考點】二次函數的性質．

【分析】由開口方向可確定a的符號，由過原點可確定常數項，則可求得其答案．

【解答】解：

設拋物線解析式為y=ax2+bx+c，

∵拋物線開中向上，

∴a＞0，故可取a=1，

∵拋物線過原點，

∴c=0，

∵對稱沒有限制，

∴可取b=1，

故答案為：y=x2+x．

【點評】本題主要考查二次函數的性質，掌握二次函數的開口方向由a的符號決定是解題的關鍵．

15．已知點A（，y1），B（﹣2，y2）都在二次函數y=（x﹣2）2﹣1的圖象上，則y1與y2的大小關系是　y1＜y2　．

【考點】二次函數圖象上點的坐標特征．

【分析】先求得函數的對稱軸為x=2，再判斷A（，y1），B（﹣2，y2）在對稱軸左側，從而判斷出y1與y2的大小關系．

【解答】解：∵函數y=（x﹣2）2﹣1的對稱軸為x=2，

∴A（，y1），B（﹣2，y2）在對稱軸左側，

∵拋物線開口向上，在對稱軸左側y隨x的增大而減小，

∵＞﹣2，

∴y1＜y2．

故答案為：y1＜y2．

【點評】此題考查了待定系數法二次函數圖象上點的特征，利用已知解析式得出對稱軸進而利用二次函數增減性得出是解題關鍵．

16．如圖，△ABC繞點A順時針旋轉45°得到△AB′C′，若∠BAC=90°，AB=AC=，則圖中陰影部分的面積等于　﹣1　．

【考點】旋轉的性質；等腰直角三角形．

【分析】根據題意結合旋轉的性質以及等腰直角三角形的性質得出AD=BC=1，AF=FC′=sin45°AC′=AC′=1，進而求出陰影部分的面積．

【解答】解：∵△ABC繞點A順時針旋轉45°得到△AB′C′，∠BAC=90°，AB=AC=，

∴BC=2，∠C=∠B=∠CAC′=∠C′=45°，

∴AD⊥BC，B′C′⊥AB，

∴AD=BC=1，AF=FC′=sin45°AC′=AC′=1，

∴圖中陰影部分的面積等于：S△AFC′﹣S△DEC′=×1×1﹣×（﹣1）2=﹣1．

故答案為：﹣1．

【點評】此題主要考查了旋轉的性質以及等腰直角三角形的性質等知識，得出AD，AF，DC′的長是解題關鍵．

三、解答題（一）：本大題共3小題，每小題6分，共18分．

17．解方程：x2﹣3x+2=0．

【考點】解一元二次方程-因式分解法．

【分析】把方程的左邊利用十字相乘法因式分解為（x﹣1）（x﹣2），再利用積為0的特點求解即可．

【解答】解：∵x2﹣3x+2=0，

∴（x﹣1）（x﹣2）=0，

∴x﹣1=0或x﹣2=0，

∴x1=1，x2=2．

【點評】本題考查了因式分解法解一元二次方程，當把方程通過移項把等式的右邊化為0后方程的左邊能因式分解時，一般情況下是把左邊的式子因式分解，再利用積為0的特點解出方程的根．因式分解法是解一元二次方程的一種簡便方法，要會靈活運用．

18．已知二次函數y=﹣x2﹣2x，用配方法把該函數化為y=a（x﹣h）2+c的形式，并指出函數圖象的對稱軸和頂點坐標．

【考點】二次函數的三種形式．

【分析】先配方，得到二次函數的頂點坐標式，即可直接寫出其對稱軸和頂點坐標．

【解答】解：y=﹣x2﹣2x，

=﹣（x2+2x）

=﹣（x2+2x+1﹣1）

=﹣（x+1）2+1

即對稱軸是直線x=﹣1，頂點坐標是（﹣1，1）．

【點評】本題考查了二次函數的性質，重點是學會由一般式向頂點坐標式的轉化．

19．已知x=1是關于x的一元二次方程x2+3x﹣m=0的一個根，求m的值和方程的另一個根．

【考點】根與系數的關系；一元二次方程的解．

【分析】由于x=1是方程的一個根，直接把它代入方程即可求出m的值，然后根據根與系數的關系可以求出方程的另一根．

【解答】解：∵x=1是方程的根，

∴1+3﹣m=0，

∴m=4，

設另一個根為x2，則1+x2=﹣3，

∴x2=﹣4，

∴m的值是4，另一個根是x=﹣4．

【點評】此題考查了一元二次方程的根的定義，把方程的根代入原方程就可以確定待定系數m的值，然后根據根與系數的關系就可以求出方程的另一個根．

四、解答題（二）：本大題3小題，每小題7分，共21分．

20．如圖，在平面直角坐標系中，已知△ABC的三個頂點的坐標分別為（﹣1，1），B（﹣3，1），C（﹣1，4）．

（1）將△ABC繞點A順時針旋轉90°后得到△AB′C′，請在圖中畫出△AB′C′．

（2）寫出點B′、C′的坐標．

【考點】作圖-旋轉變換．

【分析】（1）利用網格特點和旋轉的性質畫出點B、C的對應點B′、C′，從而得到△AB′C′；

（2）利用（1）中畫出的圖形寫出點B′、C′的坐標．

【解答】解：（1）如圖，△AB′C′為所求；

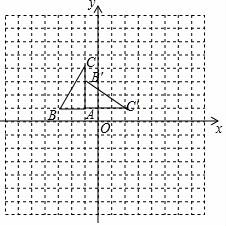
（2）B′（﹣1，3）、C′（2，1）．

【點評】本題考查了作圖﹣旋轉變換：根據旋轉的性質可知，對應角都相等都等于旋轉角，對應線段也相等，由此可以通過作相等的角，在角的邊上截取相等的線段的方法，找到對應點，順次連接得出旋轉后的圖形．

21．如圖，已知拋物線y=x2+x﹣6與x軸兩個交點分別是A、B（點A在點B的左側）．

（1）求A、B的坐標；

（2）利用函數圖象，寫出y＜0時，x的取值范圍．

【考點】拋物線與x軸的交點；二次函數的性質．

【分析】（1）令y=0代入y=x2+x﹣6即可求出x的值，此時x的值分別是A、B兩點的橫坐標．

（2）根據圖象可知：y＜0是指x軸下方的圖象，根據A、B兩點的坐標即可求出x的范圍．

【解答】21．解：（1）令y=0，即x2+x﹣6=0

解得x=﹣3或x=2，

∵點A在點B的左側

∴點A、B的坐標分別為（﹣3，0）、（2，0）

（2）∵當y＜0時，x的取值范圍為：﹣3＜x＜2

【點評】本題考查二次函數與x軸的交點問題，涉及一元二次方程的解法，根據圖象解不等式等知識．

22．向陽村2013年的人均收入為10000元，2015年人均收入為12100元，若2013年到2015年人均收入的年平均增長率相同．

（1）求人均收入的年平均增長率；

（2）2014年的人均收入是多少元？

【考點】一元二次方程的應用．

【分析】（1）經過兩次增長，求年平均增長率的問題，應該明確原來的基數，增長后的結果．設人均收入的年平均增長率為x，則經過兩次增長以后人均收入為10000（1+x）2萬元，即可列方程求解；

（2）利用求得的百分率，進一步求得2014年的人均收入即可．

【解答】解：（1）設人均收入的年平均增長率為x，依題意，得

10000（1+x）2=12100，

解得：x1=0.1=10%，x2=﹣2.1（不合題意，舍去），

答：人均收入的年平均增長率為10%；

（2）2014年的人均收入為：10000（1+x）=10000（1+0.1）=11000（元）．

【點評】本題考查了一元二次方程的運用，增長率問題的數量關系的運用，解答時根據增長率問題的數量關系建立方程是關鍵．

五、解答題（三）：本大題3小題，每小題9分，共27分．

23．如圖所示，一個農戶要建一個矩形豬舍，豬舍的一邊利用長為12m的房墻，另外三邊用25m長的建筑材料圍成，為了方便進出，在垂直于房墻的一邊留一個1m寬的門．

（1）所圍成矩形豬舍的長、寬分別是多少時，豬舍面積為80m2？

（2）為做好豬舍的衛生防疫，現需要對圍成的矩形進行硬底化，若以房墻的長為矩形豬舍一邊的長，且已知硬底化的造價為60元/平方米，請你幫助農戶計算矩形豬舍硬底化需要的費用．

【考點】一元二次方程的應用．

【分析】（1）設矩形豬舍垂直于房墻的一邊長為xm，則矩形豬舍的另一邊長為（26﹣2x）m，根據豬舍面積為80m2，列出方程并解答；

（2）若以房墻的長為矩形豬舍一邊的長，可得垂直于房墻的一邊長為7m，再根據矩形的面積公式得到矩形豬舍的面積，再根據總價=單價×數量可求矩形豬舍硬底化的造價．

【解答】解：（1）設矩形豬舍垂直于房墻的一邊長為xm，則矩形豬舍的另一邊長為（26﹣2x）m．

依題意，得x（26﹣2x）=80，

解得x1=5，x2=8．

當x=5時，26﹣2x=16＞12（舍去），

當x=8時，26﹣2x=10＜12．

答：矩形豬舍的長為10m，寬為8m．

（2）若以房墻的長為矩形豬舍一邊的長，

則26﹣2x=12，解得x=7，

∴垂直于房墻的一邊長為7m，

∴矩形豬舍的面積為：12×7=84（m2），

∴矩形豬舍硬底化的造價為：84×60=5040（元）．

答：矩形豬舍硬底化的造價是5040元．

【點評】本題考查了一元二次方程的應用，解題關鍵是要讀懂題目的意思，根據題目給出的條件，找出合適的等量關系，列出方程，再求解．

24．一塊三角形材料如圖所示，∠A=30°，∠C=90°，AB=12，用這塊材料剪出一個矩形CDEF，其中D、E、F分別在BC、AB、AC上．

（1）若設AE=x，則AF=　x　；（用含x的代數式表示）

（2）要使剪出的矩形CDEF的面積最大，點E應選在何處？

【考點】相似三角形的應用；二次函數的最值；矩形的性質．

【分析】（1）在直角三角形中，利用30度所對的直角邊等于斜邊的一半表示出EF，再利用勾股定理表示出AF即可；

（2）利用30度所對的直角邊等于斜邊的一半表示出BC，進而利用勾股定理表示出AC，由AC﹣AF表示出CF，根據CF與EF乘積列出S與x的二次函數解析式，利用二次函數性質確定出面積的最大值，以及此時x的值即可．

【解答】解：（1）在Rt△ABC中，∠A=30°，∠C=90°，AE=x，

∴EF=x，

根據勾股定理得：AF=x；

故答案為： x；

（2）∵四邊形CDEF是矩形，

∴∠AFE=90°，

∵∠A=30°，

∴EF=AE=x，

在Rt△ABC中，∠C=90°，AB=12，

∴BC=AB=6，

根據勾股定理得：AC==6，

∴CF=AC﹣AF=6﹣x，

∴S矩形CDEF=CF?EF=x（6﹣x）=﹣（x﹣6）2+9，

∴當x=6時，矩形CDEF的面積最大，

即當點E為AB的中點時，矩形CDEF的面積最大．

【點評】此題考查了相似三角形的應用，二次函數的最值，勾股定理，含30度直角三角形的性質，以及矩形的性質，熟練掌握性質及定理是解本題的關鍵．

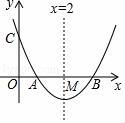
25．如圖，已知拋物線y=x2+bx+c與x軸交于點A、B，AB=2，與y軸交于點C，對稱軸為直線x=2，對稱軸交x軸于點M．

（1）求拋物線的函數解析式；

（2）設P為對稱軸上一動點，求△APC周長的最小值；

（3）設D為拋物線上一點，E為對稱軸上一點，若以點A、B、D、E為頂點的四邊形是菱形，則點D的坐標為　（2，﹣1）　．

【考點】二次函數綜合題．

【分析】（1）首先確定A、B兩點坐標，利用待定系數法即可解決問題．

（2）如圖1中，連結BC，與對稱軸交點則為點P，連接AP、AC．由線段垂直平分線性質，得AP=BP，推出CB=BP+CP=AP+CP，AC+AP+CP=AC+BC，根據“兩點之間，線段最短”，得△APC周長的最小，求出AC、BC的長即可．

（3）觀察圖象可知當點D在拋物線的頂點時，可得以點A、B、D、E為頂點的四邊形為菱形，由此即可求出點D坐標．

【解答】解：（1）拋物線與x軸交于點A、B，且AB=2，

根據對稱性，得AM=MB=1，

∵對稱軸為直線x=2，

∴OA=1，OB=3，

∴點A、B的坐標分別為（1，0）、（3，0），

把A、B兩點坐標代入y=x2+bx+c，得到，

解得，

∴拋物線的解析式為：y=x2﹣4x+3．

（2）如圖1中，連結BC，與對稱軸交點則為點P，連接AP、AC．

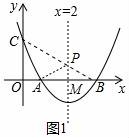
由線段垂直平分線性質，得AP=BP，

∴CB=BP+CP=AP+CP，

∴AC+AP+CP=AC+BC，

根據“兩點之間，線段最短”，得△APC周長的最小，

∵C為（0，3）

∴OC=3，

在Rt△AOC中，有AC==，

在Rt△BOC中，有BC==3，

∴△APC的周長的最小值為： +3．

（3）如圖2中，當點D為拋物線的頂點時，EM=DM時，以點A、B、D、E為頂點的四邊形是菱形，此時點D（2，﹣1）

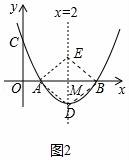
故答案為D（2，﹣1）．

【點評】本題考查二次函數綜合題、待定系數法、菱形的判定和性質、勾股定理等知識，解題的關鍵是靈活運用所學知識，學會利用對稱解決最短問題，學會利用菱形的對角線互相垂直解決問題，屬于中考壓軸題．